Un incumbent en la boleta anula sistemáticamente, y quizás hasta invierta, el infortunio electoral del partido del alcalde.

1. Réplica de Lucardi y Rosas

Intenté replicar aproximadamente tu paper con Adrián. No usé Calónico et al. para el RD — ya tendré que superar la pereza y entender sus minucias técnicas. Por ahora, estimé el switching regime model siguiente:

\(Pr(\text{win}_{t+1}=1) = \text{dneg}_t * (\alpha_0 + \alpha_2 \text{margin}_t) + (1 - \text{dneg}_t) * (\beta_0 + \beta_2 \text{margin}_t)\)

donde \(\text{dneg=1}\) indica márgenes negativos (esto es, que el partido analizado no ganó en \(t\)). Seleccioné municipios marginales donde el partido analizado ganó o fue runner-up en el año \(t\). Hice una estimación OLS con un modelo de probabilidad lineal y, para obtener errores de estimación, otra bayesiana.

Abajo aparecen las estimaciones del PAN (\(N \approx 4.7k\)). Muy parecidas entre sí y, aunque usan una serie de tiempo más larga que ustedes (1997-2023), también se parecen a sus resultados.

Tabla 1 Dos réplicas de Lucardi y Rosas
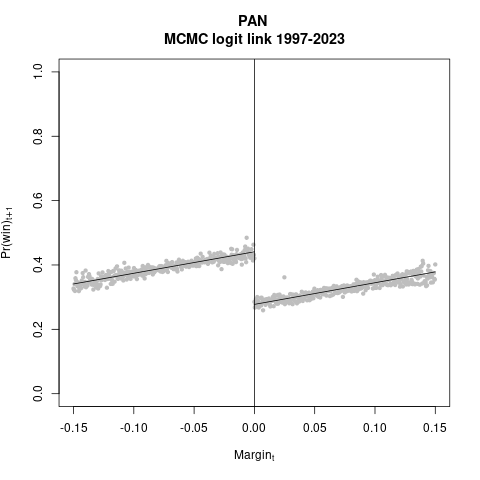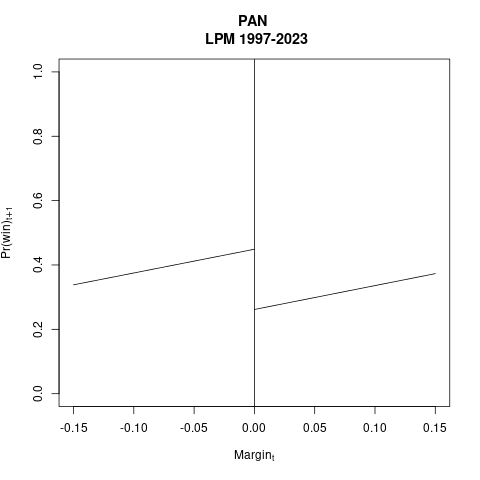pan-luro97-23-mcmc.png pan-luro97-23-lpm.png

2. Enmiendas

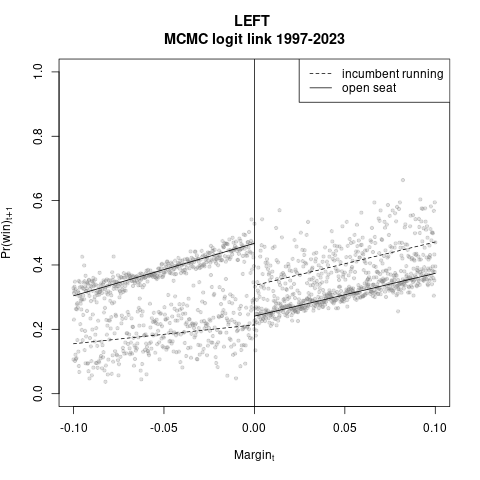
Luego hice adecuaciones. Recorté el margen a \(\pm\) 10%, como en la literatura americanista. Y metí dummies e interacciones del efecto post-reforma: el modelo lineal que cambia de régimen es \((\alpha_0 + \alpha_1 \text{dinc}_{t+1} + \alpha_2 \text{margin}_t + \alpha_3 \text{dinc}_{t+1} \times \text{margin}_t)\), donde \(\text{dinc}=1\) indica un ocupante en la boleta en t+1 (propio si el margen es positivo, ajeno si negativo). Abajo los plots de estas estimaciones.

Tabla 2 Cuando controlas la reelección consecutiva
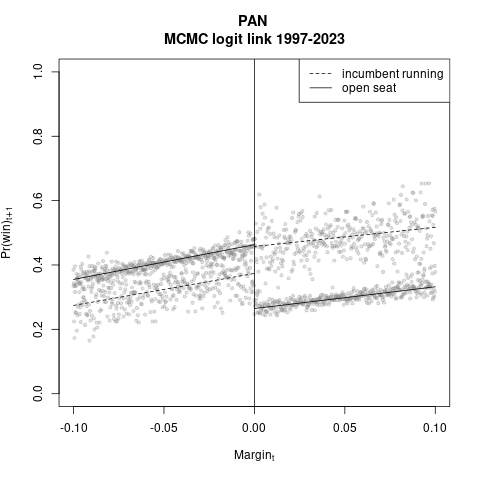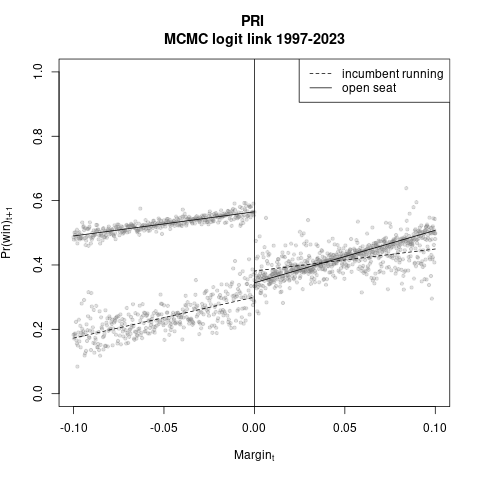pan-97-23-mcmc.png pri-97-23-mcmc.png
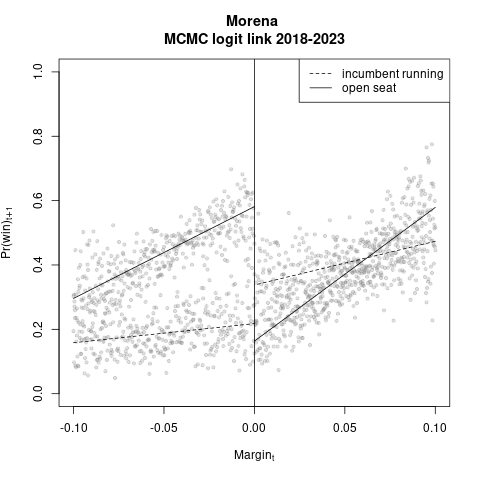left-97-23-mcmc.png left-18-23-mcmc.png

Destaca la brecha en ordenadas al origen, o sea la maldición del partido ocupante. En la lectura conservadora, con presidente municipal en la boleta desaparece en términos estadísticos. Y en todos los casos se invierte el sentido de la brecha antiocupante, aunque con evidencia mixta. Con silla vacía, β0 < α0 en la totalidad de 1,500 muestras posteriores, la maldición del partido ocupante. En cambio, cuando el presidente municipal buscó reelegirse, (β0 + β1) < (α0 + α1) en sólo la quinta parte o menos de la muestra posterior. O lo equivalente: la brecha se invierte cuatro de cinco veces, o más. No es poca cosa. Un alcalde en la boleta es una póliza de seguro contra swings partidistas negativos.

Cells report the share of the posterior sample.

  brecha sin brecha con  
  ocupante en la boleta ocupante en la boleta  
Partido β0 < α0 (β0 + β1) < (α0 + α1) N
PAN 1997-2023 1.000 0.197 4,758
PRI 1997-2023 1.000 0.146 7,293
Left 1997-2023 1.000 0.199 2,889
Left 2018-2023 1.000 0.203 394

3. Posibilidad de incidir en el ánimo contrarreformista

Además de un paper, me parece conveniente intentar publicitar este efecto. Entre los 100 comprimisos de Sheinbaum está eliminar la reelección. Si el efecto fuera real, es fácil argumentar que la contrarreforma es un tiro al pie. La reelección consecutiva como póliza de seguro contra swings partidistas negativos, como el 2021 de Morena. O como el que sufren todos al final del mandato municipal.

¿Cómo ves esto? El elefante en la habitación es la sobredeterminación: la posreforma reeleccionista coincide casi perfectamente con el colapso del sistema de partidos.

4. Duda puntual

No entiendo el criterio de selección de casos para el modelo de 'incumbents'. La nota de su TABLA 1 dice que, para estimar p(wint+1) incluyen todos los partidos ocupantes en t que también compitieron en la elección del municipio en t-1 (esto es, tres contiendas simultáneas). Esto pobla el rango positivo de margent. Con varios partidos agrupados en el análisis ¿qué es el margen negativo?

5. El modelo BUGS

###########
## MODEL ##
###########
logitModel <- function() {
    ### linear probability model with logit link
    for (n in 1:N){                ## loop over observations
        depvar[n] ~ dbern(p[n]);   
        logit(p[n]) <- inprod(beta[],X[n,]);  ## FLEXIBLE SPECIFICATION FOR VARYING N OF REGRESSORS, PREPARE depvar AND X IN R
    }
    ############################
    ## NON-INFORMATIVE PRIORS ##
    ############################
    for (k in 1:K){                ## loop over regressors
        beta[k] ~ dnorm(0, .0001);
    }
}