La medición de la historia electoral 1994–2018

(English version here.)

El propósito de esta nota es presentar, discutir y distribuir estadísticas (disponibles aquí) del desempeño electoral de los partidos en la época competitiva. Elaboro dos cantidades de interés: el pronóstico de voto con base en la historia electoral y el núcleo de apoyo de los partidos. El procedimiento que describo a continuación permite obtener medidas resumen del pasado reciente en unidades territoriales relativamente pequeñas, los municipios (\(N \approx 2,500\)) y las secciones electorales (\(N \approx 66,000\)) del país. Aplico la metodología a cuatro elecciones de diputados federales entre 2009 y 2018 (próximamente lo haré con resultados de elecciones de ayutamientos), echando mano de resultados desde 1994 como insumo histórico.

La nota empieza mostrando los estadísticos en acción. Esto permite ver su enorme potencial descriptivo y analítico. Al resumir la historia electoral reciente y su geografía, los estadísticos ofrecen una mirada panorámica a un aspecto fundamental de la política mexicana contemporánea.

Los apartados siguientes ofrecen los pormenores de la estimación de las cantidades de interés y son crecientemente técnicos.

1 Los estadísticos en acción

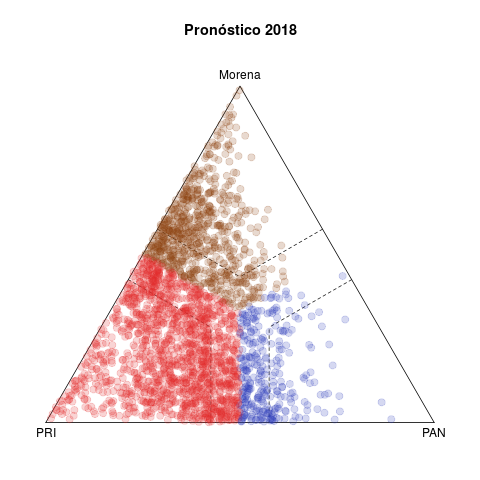
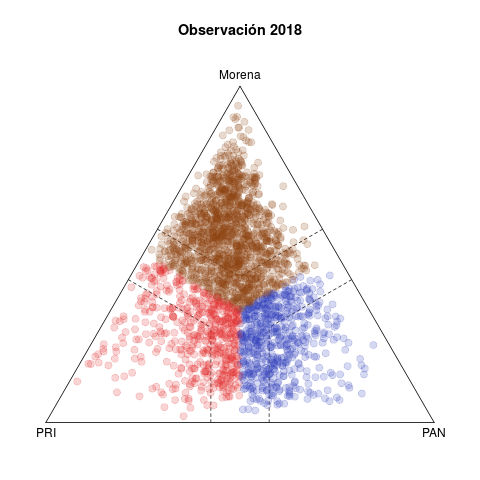
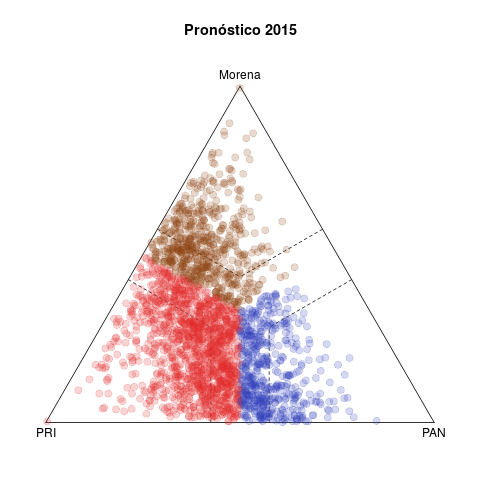
La tabla 1 presenta dos pares de diagramas de las elecciones de diputados federales de 2015 (abajo) y 2018 (arriba). Cada punto representa un municipio, coloreado según el partido que ganó la elección, y cuyas coordenas en el diagrama ternario indican el voto relativo del PAN, PRI y de la izquierda en la elección de diputados federales (no considera los votos de otros partidos).¹

Tabla 1 Expectativa histórica y voto municipal en dos elecciones federales

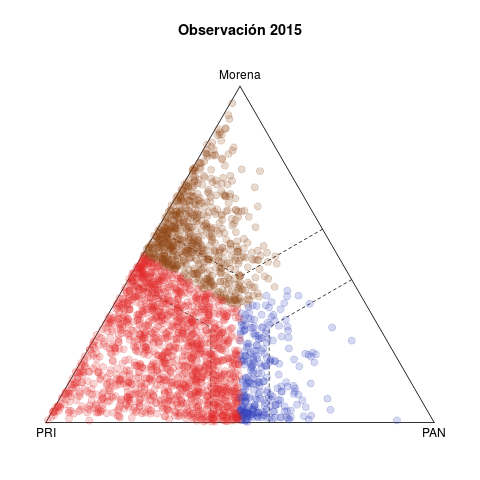Del lado izquierdo aparecen los pronósticos de voto para los municipios. La idea detrás del estadístico es resumir la evolución del voto en el municipio en cinco elecciones previas (2003–2015 en el caso de 2018) y usar la tendencia para proyectar un pronóstico de voto para 2018. Los diagramas del lado derecho, en cambio, muestran los resultados observados en ambas elecciones.

Destaco tres rasgos notables en 2018. El primero es la discrepancia entre los diagramas ternarios izquierdo y derecho. O el modelo no acierta en sus pronósticos, o la de 2018 fue una elección extraordinaria. La historia otorgaba licencia para pronosticar un triunfo holgado del PRI, tanto en número de municipios ganados como en los márgenes de victoria. Los municipios fuera de las bandas punteadas los gana un partido con un margen de 15 puntos o más, y el grueso de los municipios seguros son rojos en el pronóstico, con Morena en un distante segundo lugar. En los hechos, si bien un número no insignificante de municipios migraron hacia el PAN, la clara ventaja la demostró Morena. El underachiever fue el PRI. En contraste, los diagramas inferiores izquierdo y derecho presentan diferecias menores—2015 fue una elección normal, el pasado permitió pronosticar mejor.

Segundo, las aristas y los vértices del triángulo 2018 se despoblaron en los hechos. En los vértices se ubican municipios "zapato", sin competencia. Las aristas, en cambio, capturan bipartidismo más (dentro de las bandas punteadas) o menos (fuera) simétrico. Destaca en los pronósticos que sólo la arista PAN–Morena se esperaba desierta. En la práctica, el voto del tercer partido nunca se anuló, hubo más descoordinación que en el pasado. De hecho la intersección de las bandas punteadas aparece más densa y homogénea en el diagrama derecho que en el izquierdo.

Tercero, la competencia PAN vs izquierda fue moneda corriente en 2018. El patrón de los municipios competidos de las últimas dos décadas, visible en los diagramas de 2015, involucraba rivalidades PRI–PAN o PRI–izquierda, y rara vez PAN–izquierda. Fue esto lo que posibilitó las alianzas que formaron PAN y PRD en elecciones subnacionales desde 2010 y que culminaron en el Frente de 2018.

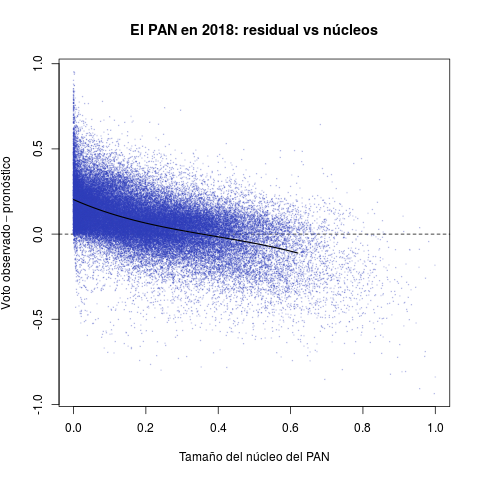
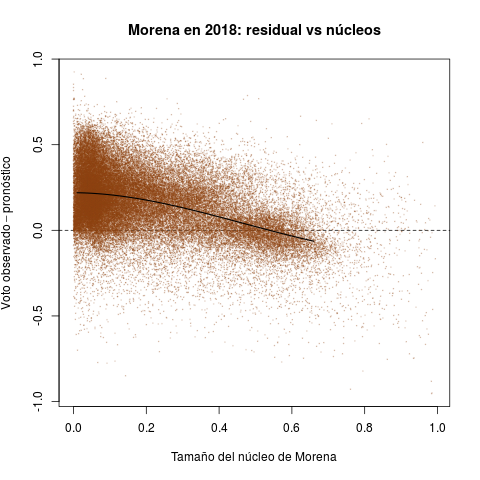
Los diagramas de la Tabla 2 reportan secciones electorales y por ello ofrecen retratos de grano mucho más fino que los anteriores. Permiten introducir la otra cantidad de interés para esta nota: el núcleo de apoyo de los partidos. La idea del estadístico es medir el tamaño del grupo que históricamente ha apoyado al partido consistentemente, en las buenas y en las malas.

Tabla 2 Núcleo de apoyo y desempeño de los partidos en 2018

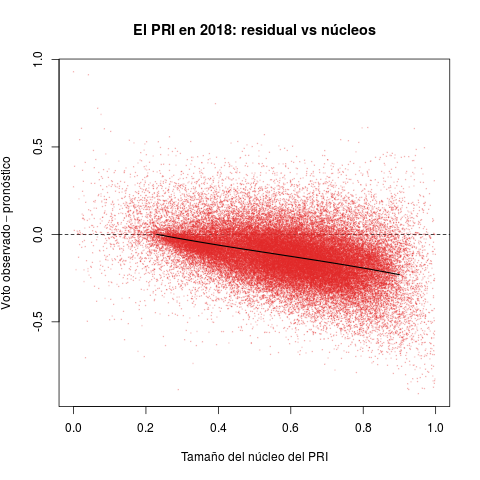El eje horizontal de cada diagrama mide el tamaño estimado del núcleo de apoyo de cada partido como proporción del electorado de la sección. El PRI aventajó a los demás en el periodo, gozó de núcleos en todas las secciones del país. Las distribuciones del PAN y de la izquierda, en cambio, aparecen desplazadas hacia el cero del eje—son reativamente pocas las secciones donde contaron con apoyo incondicional.

El eje vertical reporta el desempeño de los tres partidos en 2018 (la diferencia entre el voto observado y el pronóstico). Valores positivos indican que el partido superó las expectativas en la sección, negativos que quedó a deber. El desastre electoral del PRI se aprecia claro en el diagrama rojo. Aunque hubo secciones con desempeño positivo, la densidad se concentra masivamente debajo de la línea horizontal del cero, algo que la Tabla 1 ya dejaba entrever. Lo verdaderamente sorprendente es que el pésimo desempeño es directamente proporcional al tamaño del núcleo priista. Peña y Meade consiguieron lo que parecía, si no imposible, sí extremadamente improbable: enajenar a los votantes incondicionales del PRI en 2018. El PAN y la izquierda, en cambio, cumplieron con el pronóstico en secciones donde han contado con algunos grupos de apoyo. Ambos (sobretodo Morena) excedieron pronósticos donde carecen de núcleos importantes, arrabatándole al PRI sus votantes.

La nota elabora ahora sobre la cocina de los estadísticos (el código para replicarlos se encuentra aquí).

2 Primeras diferencias

La aproximación más común para estudiar el movimiento electoral son las primeras diferencias. Si se denota \(v_t\) a la proporción del voto de un partido en el municipio, sección u otra unidad de agregación en el periodo \(t\), la primera diferencia se define como \(d_t = v_t - v_{t-1}\).

La cantidad \(d_t\) es intuitiva, muestra el signo y la magnitud del cambio de una elección a la siguiente. Pero, porque contempla sólo pares de elecciones consecutivas, se le escapan procesos más dinámicos en las unidades. Un ejemplo, bien documentado por la sociología del voto, es la regresión a la media (Campbell 1991, Segovia 1979). Detectarlo requiere observar por lo menos tres periodos consecutivos para constatar signos contrarios en \(d_{t+1}\) y \(d_t\). Los procesos de cambio seculares de nuestro sistema de partidos en el último cuarto de siglo exigen más perspectiva histórica.

(Las primeras diferencias aparecen en los campos d.pan, d.pri y d.morena de los datos distribuidos.)

3 La tendencia lineal reciente

Un modo de adoptarla es con el pronóstico de voto a partir de la tendencia discernible en las cinco elecciones federales previas (Magar 2012). Resumo la tendencia central del voto histórico reciente mediante una estimación lineal en el tiempo, ajustando una recta por año analizado para cada partido en cada municipio o sección electoral.

La pendiente de la recta ajustada (la tendencia) permite extrapolar el apoyo electoral del partido hacia el futuro. Por ejemplo, para obtener el voto que el pasado reciente de un partido permite esperar para la unidad \(u\) en 2018, estimo la ecuación 1

\[v_{ut} = a + b \times t + \text{error}, \; t = 2003, \ldots, 2015\]

que posteriormente uso para pronosticar \(\hat{v}_{u2018} = \hat{a} + \hat{b} \times 2018\). Esta es una predicción allende la muestra (out of sample prediction) del voto esperado que puede constrastarse con el voto observado para evaluar si éste parece o no ajustarse al patrón histórico. Para el pronóstico de 2015 la muestra se desplaza un periodo y sería \(t = 2000, \ldots, 2012\), y así sucesivamente para años anteriores. Distribuyo pronósticos de voto para 2009, 2012, 2015 y 2018, producirlos conllevó estimar alrededor de diez mil regresiones municipales y más de 250 mil seccionales.

(El pronóstico de voto aparece en los campos vhat.pan, vhat.pri y vhat.morena de los datos distribuidos.)

4 El núcleo de apoyo del partido

El otro estadístico histórico es el apoyo nuclear del partido en la unidad. Su definición se desprende de clasificar el electorado en tres categorías: (1) los grupos de apoyo, que en el pasado han apoyado al partido consistentemente; (2) los grupos opositores, que han apoyado consistentemente a otro partido; y (3) los grupos swing, que no han sido consistentemente apoyo ni consistentemente opositores (Cox y McCubbins 1986). El núcleo partidista lo conforman los grupos de apoyo.

Para estimar este núcleo sigo el procedimiento de Díaz Cayeros et al. (2016). Si \(\bar{v}_t\) denota el apoyo promedio de un partido en todas las unidades en el periodo \(t\),² para cada partido en cada unidad ajusto la ecuación 2 \[\begin{equation} v_{ut} = \alpha + \beta \times \bar{v}_t + \text{error}, \; t = 1994, \ldots, 2018. \end{equation}\] \(\beta\) mide el efecto de las mareas nacionales sobre el voto del partido en la unidad \(u\). Por ejemplo, \(\hat{\beta}=1\) estimaría que por cada punto porcentual que el partido ganó o perdió a nivel nacional en el periodo, ganó o perdió un punto porcentual en la unidad; \(\hat{\beta}=0\), en cambio, indicaría un aislamiento cabal de la unidad de los cambios nacionales. Es una medida de volatilidad del voto partido en el municipio o sección (análogo a la "volatilidad beta" de la literatura financiera).

El coeficiente \(\alpha\) estima el núcleo: el apoyo esperado en \(u\) en el hipotético caso de que el partido no recibiera ningún voto a nivel nacional. Por ejemplo, \(\hat{\alpha}=.4\) indicaría que, llueve, truene o relampaguee, 40% del electorado del municipio es incondicional al partido—lo cual indicaría un núcleo de tamaño considerable.

Una crítica anticipable a esta medición del núcleo es su carácter contrafactual extremo (King y Zeng 2006). Amerita un escrutinio riguroso, que planeo llevar a cabo en el futuro.

(El núcleo de los partidos aparece en los campos alphahat.pan, alphahat.pri y alphahat.morena de los datos distribuidos. La volatiiad partidista en betahat.pan, betahat.pri y betahat.morena.)

5 Variables composicionales

Cierro con un rasgo importante de la especificación de los modelos, asociado con la naturaleza del voto como variable composicional. Las variables composicionales son descripciones cuantitativas de las partes de un todo y, por ende, tienen dos características: son proporciones que suman la unidad.³

Al estimar por separado a los partidos, el reto de las ecuaciones 1 y 2 es no pronosticar proporciones de voto menores a cero ni mayores a uno; y que la suma de pronósticos partidistas sume la unidad. Para conseguirlo, Aitchison (1986) propone sustituir las proporciones por log-relaciones (log-ratios) en el análisis. Tomando arbitrariamente al PRI como partido de referencia, define el voto del partido \(p\) con relación al PRI como \[r_p = \frac{v_p}{v_{\text{pri}}}.\] Un valor \(r_p=1\) indicaría un empate entre el partido y el PRI, mientras \(r_p>1\) que superó al PRI en la proporción que indica el valor.

Así, la ecuación 1 se reespecifica como sigue \[\ln r_{put} = a + b \times t + \text{error}\] y la ecuación 2 como \[\ln r_{put} = \alpha + \beta \times \bar{r}_{pt} + \text{error}.\]

Aplicar el logaritmo natural permite atenuar el efecto de valores extremos del regresor sobre la variable dependiente, similar como lo hace un logit. Los modelos se estimaron con mínimos cuadrados ordinarios.

Los coeficientes estimados necesitan transformarse para recuperar las proporciones de voto de los partidos. Ilustrando con el caso tripartidista, es trivial mostrar que

\begin{equation} \hat{v}_p = \frac{\hat{r}_p}{1 + \hat{r}_{\text{pan}} + \hat{r}_{\text{morena}}} \; \text{y} \; \hat{v}_{\text{pri}} = \frac{1}{1 + \hat{r}_{\text{pan}} + \hat{r}_{\text{morena}}.} \end{equation}

Estas son las cantidades que reportan los datos distribuidos.

6 Referencias

• Aitchison, John. 1986. The Statistical Analysis of Compositional Data. Nueva York: Chapman and Hall.
• Campbell, James E. 1991. The presidential surge and its midterm decline in congressional elections, 1868-1988. The Journal of Politics 53(2):477-87.
• Cox, Gary W. y Mathew D. McCubbins. 1986. Electoral Politics as a Redistributive Game. The Journal of Politics 48(2):370-89.
• Díaz Cayeros, Alberto, Federico Estévez y Beatriz Magaloni. 2016. The Political Logic of Poverty Relief: Electoral Strategies and Social Policy in Mexico. Nueva York: Cambridge University Press.
• King, Gary y Langche Zeng. 2006. The Dangers of Extreme Counterfactual. Political Analysis 14(2):131-59.
• Magar, Eric. 2012. Gubernatorial Coattails in Mexican Congressional Elections. The Journal of Politics 74(2):383-99.
• Segovia, Rafael. 1979. Las elecciones federales de 1979. Foro Internacional 20(3):397-410.

Nota al pie de página:

¹

Cabe aclarar que, para la historia electoral de la izquierda (que denomino "Morena" en los diagramas y los datos distribuidos), agregué sistemáticamente los votos del PRD, PT y MC hasta 2015. Ese año, a los tres les sumé los votos de Morena y del PES. En 2018 la izquierda la conformaron Morena, PT y PES.

²

Habría que omitir la unidad \(u\) analizada del promedio del año \(t\) para no incluir la variable dependiente de ambos lados de la ecuación. No lo hago porque, dado el grande número de unidades muinicipales o seccionales, y tratándose de datos relativos de cada unidad, este refinamiento tendría un impacto ínfimo en el valor de cada promedio.

³

Formalmente, las composicionales son variables aleatorias sujetas a dos restricciones: \[0 \leq v_p \leq 1 \; \forall \; p \in P \; \;\] y \[\; \; \sum_P v_p = 1.\]